CUALITATIVA Y
MATEMÁTICA
VORTICIAL
 | ARITMÉTICA CUALITATIVA Y MATEMÁTICA VORTICIAL |
⟨( n/(módulo(m)) = n − m*(n÷m) )⟩
15/(módulo(12)) = 15 − 12*(15÷12) = 15 − 12*1 = 3
12/(módulo(12)) = 12 − 12*(12÷12) = 12 − 12*1 = 0
rd(r) a la función “raíz digital” de un número r, tenemos los ejemplos:
rd(23) = 5
rd(1234) = rd(10) = 1
rd(12.75) = rd(15) = 6
r:
⟨( rd(r) = r − 9*((r−1)÷9) )⟩
rd(15) = 15 − 9*(15÷9) = 15 − 9*1 = 6
rd(9) = 9 − 9*(8÷9) = 9 − 9*0 = 9
rd(10) = 10 − 9*(10÷9) = 10 − 9*1 = 1
r para obtener su raíz digital se denomina “persistencia aditiva” de r. Llamando pa(r) a la función “persistencia aditiva” de r, tenemos:
pa(23) = 1
pa(1234) = 2
pa(12.75) = 2
pa(5) = 0
⟨( (−d = 9−d) ← d≠9 →' 9 )⟩
−1=8 −2=7 −3=6
−4=5 −5=4 −6=3
−7=2 −8=1 −9=9
⟨( −(−d) = d )⟩
⟨( (−d1 = d2)→ (−d2 = d1) )⟩
⟨( d−d = 9 )⟩
⟨( (rd(d) = 9−d) ← d<0 )⟩
rd(−5) = 9−5 = 4 rd(−9) = 9
⟨( rd(−r) = −rd(r) )⟩
rd(−123) = −rd(123) = −rd(6) = −6 = 9−6 = 3
⟨( rd(n)=n ↔ n∈{1…9} )⟩
rd(5) = 5
⟨( rd(r+9) = rd(r) )⟩
rd(43+9) = rd(52) = 7 = rd(43)
rd(45.3+9) = rd(54.3) = 3 = rd(45.3)
⟨( rd(r*9) = 9 )⟩
rd(45*9) = rd(405) = 9
rd(45.3*9) = rd(407.7) = rd(18) = 9
⟨( rd(r1+r2) = rd(rd(r1)+rd(r2)) )⟩
rd(451+137) = rd(588) = rd(21) = 3
rd(rd(451)+rd(137)) = rd(10+11) = rd(21) = 3
⟨( rd(r1−r2) = rd(rd(r1)−rd(r2)) )⟩
rd(451−137) = rd(314) = 8
rd(rd(451)−rd(137)) = rd(10−11) = rd(−1) = 9−1 = 8
⟨( rd(r1*r2) = rd(rd(r1)*rd(r2)) )⟩
rd(45*13) = rd(585) = rd(18) = 9
rd(rd(45)*rd(13)) = rd(9*4) = rd(36) = 9
⟨( rd(10^n) = 1 )⟩
⟨( rd(r*(10^n)) = r )⟩
⟨( rd(n−inverso(n)) = 9 )⟩
rd(531−135) = rd(396) = 9
rd(135−531) = rd(−396) = −rd(396) = −9 = 9
⟨( (rd(n) ∈ {1 4 7}) → (rd(n*3) = 3) )⟩
⟨( (rd(n) ∈ {2 5 8}) → (rd(n*3) = 6) )⟩
⟨( (rd(n) ∈ {3 6 9}) → (rd(n*3) = 9) )⟩
rd(127) = rd(10) = 1 rd(127*3) = rd(381) = 3
rd(128) = rd(11) = 2 rd(128*3) = rd(384) = 6
rd(129) = rd(12) = 3 rd(129*3) = rd(387) = 9
⟨( (rd(n) ∈ {1 4 7}) → (rd(n*6) = 6) )⟩
⟨( (rd(n) ∈ {2 5 8}) → (rd(n*6) = 3) )⟩
⟨( (rd(n) ∈ {3 6 9}) → (rd(n*6) = 9) )⟩
rd(127) = rd(10) = 1 rd(127*6) = rd(762) = 6
rd(128) = rd(11) = 2 rd(128*6) = rd(768) = 3
rd(129) = rd(12) = 3 rd(129*6) = rd(774) = 9
⟨rd(r+9)⟩ = rd(r) es análoga a ⟨(r+0 = r)⟩ de la aritmética cuantitativa.
⟨(rd(r*9) = 9)⟩ es análoga a ⟨(r*0 = 0)⟩ de la aritmética cuantitativa.
| + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 |
| 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| − | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 2 | 1 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
| 3 | 2 | 1 | 9 | 8 | 7 | 6 | 5 | 4 | 3 |
| 4 | 3 | 2 | 1 | 9 | 8 | 7 | 6 | 5 | 4 |
| 5 | 4 | 3 | 2 | 1 | 9 | 8 | 7 | 6 | 5 |
| 6 | 5 | 4 | 3 | 2 | 1 | 9 | 8 | 7 | 6 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 9 | 8 | 7 |
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 9 | 8 |
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 9 |
⟨( d1−d2 = d1 + (−d2) )⟩,
⟨( d1−d2 = d1 + (9 − d2) )⟩
|
| |||||
|
| |||||
|
| |||||
|
| |||||
|
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 1 | 3 | 5 | 7 | 9 |
| 3 | 3 | 6 | 9 | 3 | 6 | 6 | 3 | 6 | 9 |
| 4 | 4 | 8 | 3 | 7 | 2 | 6 | 1 | 5 | 9 |
| 5 | 5 | 1 | 6 | 2 | 7 | 3 | 8 | 4 | 9 |
| 6 | 6 | 3 | 9 | 6 | 3 | 9 | 6 | 3 | 9 |
| 7 | 7 | 5 | 3 | 1 | 8 | 6 | 4 | 2 | 9 |
| 8 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 9 |
| 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
⟨( rd(8*d) = −d )⟩ p.e. rd(8*5)=4 rd(8*3)=6
|
| |||||
|
| |||||
|
| |||||
|
| |||||
|
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1÷d | 1 | 5 | − | 7 | 2 | − | 4 | 8 | − |
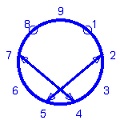
|
| Diagrama de inversos |
rd(r1÷r2) = rd(rd(r1)÷rd(r2))
rd(1÷4) = rd(0.25) = 7
rd(1÷8) = rd(0.125) = 8
rd(124÷47) = rd(7÷11) = rd(7÷2) = rd(3.5) = 8
rd(10÷8) = rd(1.25) = 8
rd(100÷3) no está definida
| ^ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 4 | 8 | 7 | 5 | 1 | 2 | 4 | 8 |
| 3 | 3 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| 4 | 4 | 7 | 1 | 4 | 7 | 1 | 4 | 7 | 1 |
| 5 | 5 | 7 | 8 | 4 | 2 | 1 | 5 | 7 | 8 |
| 6 | 6 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| 7 | 7 | 4 | 1 | 7 | 4 | 1 | 7 | 4 | 1 |
| 8 | 8 | 1 | 8 | 1 | 8 | 1 | 8 | 1 | 8 |
| 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 |
| 2 | 3 | 5 | 7 | 2 | 4 | 8 | 1 | 5 | 2 | 4 | 1 | 5 | 7 | 2 | 8 | 5 | 7 | 4 |
| 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 |
| 8 | 1 | 7 | 2 | 8 | 7 | 2 | 4 | 8 | 1 | 5 | 1 | 5 | 2 | 4 | 5 | 7 | 4 | 1 |
| 167 | 173 | 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 |
| 5 | 2 | 8 | 1 | 2 | 4 | 8 | 1 | 4 | 7 | 2 | 4 | 8 | 5 | 7 | 8 | 5 | 2 | 8 |
| 271 | 277 | 281 | 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 | 367 | 373 | 379 | 383 |
| 1 | 7 | 2 | 4 | 5 | 1 | 5 | 7 | 2 | 7 | 4 | 5 | 7 | 2 | 8 | 7 | 4 | 1 | 5 |
| 389 | 397 | 401 | 409 | 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 | 467 | 479 | 487 | 491 | 499 |
| 2 | 1 | 5 | 4 | 5 | 7 | 8 | 1 | 7 | 2 | 8 | 7 | 2 | 4 | 8 | 2 | 1 | 5 | 4 |
| 503 | 509 | 521 | 523 | 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 | 601 | 607 | 613 | 617 | 619 |
| 8 | 5 | 8 | 1 | 1 | 7 | 8 | 5 | 2 | 4 | 1 | 2 | 8 | 5 | 7 | 4 | 1 | 5 | 7 |
| 631 | 641 | 643 | 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 733 | 739 | 743 | 751 |
| 1 | 2 | 4 | 8 | 5 | 2 | 4 | 7 | 2 | 8 | 7 | 8 | 7 | 8 | 7 | 4 | 1 | 5 | 4 |
| 757 | 761 | 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 |
| 1 | 5 | 4 | 8 | 4 | 5 | 8 | 1 | 2 | 4 | 8 | 2 | 2 | 7 | 2 | 4 | 8 | 4 | 8 |
| 883 | 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 | |||
| 1 | 5 | 7 | 2 | 1 | 2 | 1 | 5 | 2 | 8 | 4 | 8 | 5 | 2 | 1 | 7 |
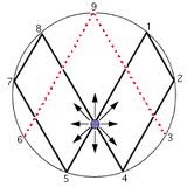
|
| Los dos patrones fundamentales de la matemática vorticial |
| 5 | 7 | 8 | 4 | 2 | 1 |
| 6 | 9 | 3 | 3 | 9 | 6 |
| 1 | 2 | 4 | 8 | 7 | 5 |
|
|
| 8 | 7 | 5 | 1 |
| 8 | 4 | 2 | 1 |

|
| El símbolo de la fe Baha'i |
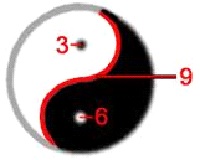
|
| El yin-yang de la aritmética cualitativa |
|
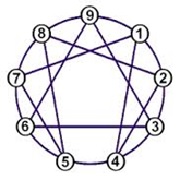
| El Eneagrama |
|
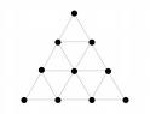
| La Tetraktys pitagórica |

|
| El símbolo de la matemática vorticial |

|
| El símbolo de la masonería |
|
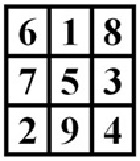
| Cuadrado mágico Luo Shu |